Las compuertas lógicas son dispositivos que operan con aquellos estados lógicos mencionados en lo anterior y funcionan igual que una calculadora, de un lado ingresas los datos, ésta realiza una operación, y finalmente, te muestra el resultado.
 

​

​

​

​

​

​

​

Cada una de las compuertas lógicas se las representa mediante un Símbolo, y la operación que realiza (Operación lógica) se corresponde con una tabla, llamada Tabla de Verdad, veamos la primera.



Compuerta NOT



Se trata de un inversor, es decir, invierte el dato de entrada, por ejemplo; si pones su entrada a 1 (nivel alto) obtendrás en su salida un 0 (o nivel bajo), y viceversa. Esta compuerta dispone de una sola entrada. Su operación lógica es s igual a a invertida

​

​

​

​

​

​

​
 

Compuerta AND



Una compuerta AND tiene dos entradas como mínimo y su operación lógica es un producto entre ambas, no es un producto aritmético, aunque en este caso coincidan.*Observa que su salida será alta si sus dos entradas están a nivel alto*
 

​

​

​

​

​

​

​

​

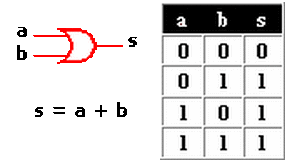
Compuerta OR



Al igual que la anterior posee dos entradas como mínimo y la operación lógica, será una suma entre ambas... Bueno, todo va bien hasta que 1 + 1 = 1, el tema es que se trata de una compuerta O Inclusiva es como a y/o b*Es decir, basta que una de ellas sea 1 para que su salida sea también 1*
 

​

​

​

​

​

​

​

​

​

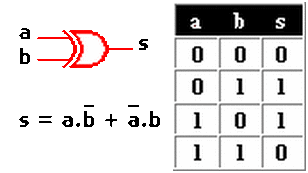
Compuerta OR-EX o XOR



Es OR EXclusiva en este caso con dos entradas (puede tener más) y lo que hará con ellas será una suma lógica entre a por b invertida y a invertidapor b.*Al ser O Exclusiva su salida será 1 si una y sólo una de sus entradas es 1*

​
 

​

​

​

​

​

​

​

Estas serían básicamente las compuertas más sencillas.



Compuertas Lógicas CombinadasAl agregar una compuerta NOT a cada una de las compuertas anteriores los resultados de sus respectivas tablas de verdad se invierten, y dan origen a tres nuevas compuertas llamadas NAND, NOR y NOR-EX. Veamos ahora como son y cuál es el símbolo que las representa...







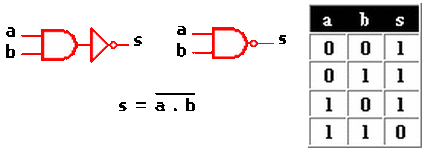
Compuerta NAND



Responde a la inversión del producto lógico de sus entradas, en su representación simbólica se reemplaza la compuerta NOT por un círculo a la salida de la compuerta AND.

 

 

 

 

 

 

 

 

 

 

Compuerta NOR



El resultado que se obtiene a la salida de esta compuerta resulta de la inversión de la operación lógica o inclusiva es como un no a y/o b. Igual que antes, solo agregas un círculo a la compuerta OR y ya tienes una NOR.

 

 

 

 

 

 

 

 

 

 

Compuerta NOR-EX



Es simplemente la inversión de la compuerta OR-EX, los resultados se pueden apreciar en la tabla de verdad, que bien podrías compararla con la anterior y notar la diferencia, el símbolo que la representa lo tienes en el siguiente gráfico.

 

 

 

 

 

 

 

 

 




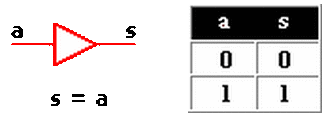
Buffer's



En realidad no realiza ninguna operación lógica, su finalidad es amplificar un poco la señal (o refrescarla si se puede decir). Como puedes ver en el siguiente gráfico la señal de salida es la misma que de entrada.























4.3.1 Mini y maxi términos.

MINITÉRMINO (mi): Término producto en el que aparecen todas las variables, yasean complementadas o sin complementar.

FÓRMULA CANÓNICA DISYUNTIVA O DE MINITÉRMINOS

suma de mintérminos (Suma de Productos).Dada la lista completa de mintérminos y asignando 1's y 0's arbitrariamente a las variables, siempre hay un, y sólo un, minitérmino que toma el valor 1. Un mintérmino es un término producto que es 1 exactamente en una línea de la tabla de Verdad.La fórmula compuesta por todos los mintérminos será idénticamente 1. Cada fórmula de conmutación puede expresarse como suma de mintérminos. Y esa fórmula es única.

Algunas veces es conveniente expresar la función booleana en la forma de suma de miniterminos.  Si no puede hacerse en esta forma entonces puede realizarse primero por la expansión de la expresión en una suma de los términos AND.

Después cada término se inspecciona para ver si contiene todas las variables, si se han perdido una o más variables, se aplica el operador AND con una expresión x+x’ en donde x es una de las variables perdidas.

NOTACIÓN: Un mintérmino se designa por "mi" siendo i el número decimal correspondiente de la tabla de verdad. Para el producto, el 0 se asocia a la variable complementada y el 1 a la variable sin complementar.

 

EJEMPLO:C B A F(C,B,A)
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1

F(C,B,A) = m0 + m2 + m3 +m7 = S m(0,2,3,7)
F(C,B,A) = C'·B'·A' + C'·B·A' + C'·B·A + C·B·A
O bien
F(C,B,A) = C·B·A + C·B·A + C·B·A + C·B·A



Ejemplo:  Expresar la función  F = A+B’C en una suma de miniterminos.



F= A+B’C
F(A,B,C)
A= A(B+B’) = AB+AB’
  = AB(C+C’) + AB’(C+C’)
  = ABC + ABC’ + AB’C +AB’C’



B’C = B’C (A+A’)

      = AB’C + A’B’C

F = ABC+ABC’+AB’C+AB’C’+AB’C+A’B’C
F = A’B’C+AB’C’ +AB’C+ABC’+ABC
F = m1+ m4+m5+ m6+ m7
F(A,B,C)=SUM(1,4,5,6,7)

La sumatoria representa al operador OR que opera en los términos y números siguientes son los minitérminos de la función.

Las letras entre paréntesis que siguen a F forman una lista de las variables en el orden tomado cuando el minitérmino se convierte en un término AND.

 

MAXTÉRMINO (Mi): término suma en el que aparecen todas las variables, ya sean complementadas o sin complementar.

FÓRMULA CANÓNICA CONJUNTIVA O DE MAXTÉRMINOS: producto de maxtérminos (Producto de sumas).

Dada la lista completa de maxtérminos y asignando 1¶s y 0¶s arbitrariamente a las variables, siempre hay un y sólo un maxtérmino que toma el valor 0. Un maxtérmino es un término suma que es 0 exactamente en una línea de la tabla de verdad. La fórmula compuesta por todos los maxtérminos será idénticamente 0. Cada fórmula puede expresarse como producto de maxtérminos. Y es única. NOTACIÓN: Un maxtérmino se designa por ³Mi´ siendo i el número decimal correspondiente de la tabla de verdad. En la suma, el 1 se asocia a la variable complementada y el 0 a la variable sin complementar.

EJEMPLO:C B A F(C,B,A)
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1

F(C,B,A) = M1 · M4 · M5 · M6 = P M(1,4,5,6)
F(C,B,A) = (C+B+A') · (C'+B+A) · (C'+B+A') · (C'+B'+A)
O bien:

F(C,B,A) = (C+B+A) · (C+B+A) · (C+B+A) · (C+B+A)



4.3.2 Representación de expresiones booleanas con circuitos lógicos​



































​