​1.1-Sistemas Numéricos
Los sistemas de numeración son conjuntos de dígitos usados para
representar cantidades, así se tienen los sistemas de numeración
decimal, binario, octal, hexadecimal, romano, etc. Los cuatro primeros
se caracterizan por tener una base (número de dígitos diferentes: diez,
dos, ocho, dieciseis respectivamente) mientras que el sistema romano
no posee base y resulta más complicado su manejo tanto con
números, así como en las operaciones básicas.
Los sistemas de numeración que poseen una base tienen la
característica de cumplir con la notación posicional, es decir, la
posición de cada número le da un valor o peso, así el primer dígito de
derecha a izquierda después del punto decimal, tiene un valor igual a
b veces el valor del dígito, y así el dígito tiene en la posición n un valor
igual a: (b n) * Adonde:
b = valor de la base del sistema
n = número del dígito o posición del mismo
A = dígito.

Por ejemplo:
digitos: 1 2 4 9 5 3 . 3 2 4
posicion 5 4 3 2 1 0 . -1 -2 -3

Clasificación
Los sistemas de numeración pueden clasificarse en dos grandes
grupos: posicionales y no-posicionales:
  En los sistemas no-posicionales los dígitos tienen el valor del
símbolo utilizado, que no depende de la posición (columna) que
ocupan en el número.
  En los sistemas de numeración ponderados o posicionales el
valor de un dígito depende tanto del símbolo utilizado, como de
la posición que ése símbolo ocupa en el número.
Por ejemplo, el sistema de  numeración egipcio es no posicional, en
cambio el  babilónico es posicional.

​

Las  lenguas naturales poseen sistemas de numeración posicionales basados en base 10 ó 20, a
veces con subsistemas de cinco elementos. Además, en algunas
pocas lenguas los  numerales básicos a partir de cuatro tienen
nombres basados en numerales más pequeños.

Sistemas de numeración no posicionales
Estos son los más primitivos se usaban por ejemplo los dedos de la
mano para representar la cantidad cinco y después se hablaba de
cuántas manos se tenía. También se sabe que se usaba cuerdas con
nudos para representar cantidad. Tiene mucho que ver con la
coordinabilidad entre conjuntos. Entre ellos están los sistemas del
antiguo Egipto, el sistema de  numeración romana, y los usados en
Mesoamérica por mayas, aztecas y otros pueblos .
Al igual que otras civilizaciones mesoamericanas, los mayas utilizaban
un sistema de numeración de raíz mixta de base 20 (vigesimal).
También los mayas preclásicos desarrollaron independientemente el
concepto de cero alrededor del año 36 a. C.1 Este es el primer uso
documentado del cero en América, aunque con algunas peculiaridades
que le privaron de posibilidad operatoria.2 Las inscripciones, los
muestran en ocasiones trabajando con sumas de hasta cientos de
millones y fechas tan extensas que tomaba varias líneas el poder
representarlas.

Sistemas de numeración posicionales

El número de símbolos permitidos en un sistema de numeración
posicional se conoce como  base del sistema de numeración. Si un
sistema de numeración posicional tiene base  b significa que
disponemos de b símbolos diferentes para escribir los números, y que
b unidades forman una unidad de orden superior.

1.1.1- Sistemas numéricos (Binario, Decimal, Octal y Hexadecimal)​

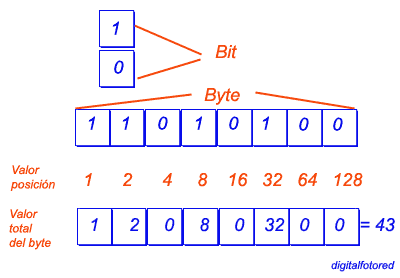
SISTEMA BINARIO
El sistema binario, en matemáticas e informática, es un sistema de numeración
en el que los números se representan utilizando solamente las cifras cero y uno (0
y 1). Es el que se utiliza en las computadoras, debido a que trabajan internamente
con dos niveles  de  voltaje, por lo cual su sistema de numeración natural es el
sistema binario (encendido 1, apagado 0).Un número binario puede ser representado por cualquier secuencia de bits (dígitos
binarios), que suelen representar cualquier mecanismo capaz de usar dos estados
mutuamente excluyentes. Las siguientes secuencias de símbolos podrían ser
interpretadas como el mismo valor numérico binario:
1 0 1 0 0 1 1 0 1 0
| - | - - | | - | -
x o x o o x x o x o
y n y n n y y n y n

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

SISTEMA DECIMAL
El  sistema de numeración decimal, también llamado  sistema
decimal, es un  sistema de numeración posicional en el que las
cantidades se representan utilizando como  base aritmética las
potencias del número diez. El conjunto de símbolos utilizado (sistema
de numeración arábiga) se compone de diez cifras diferentes: cero (0);
uno (1); dos (2); tres (3); cuatro (4); cinco (5); seis (6); siete (7); ocho
(8) y nueve (9).
Al ser posicional, el sistema decimal es un sistema de numeración en
el cual el valor de cada dígito depende de su posición dentro del
número. Al primero corresponde el lugar de la unidades, el dígito se
multiplica por 10° (es decir 1) ; el siguiente las decenas (se multiplica
por 10); centenas (se multiplica por 100); etc. Ejemplo:

​























SISTEMA OCTAL
El sistema numérico octal utiliza como base el 8 que corresponde al
número de dígitos que se utilizan para representar cantidades. Estos
dígitos son 0, 1, 2, 3, 4, 5, 6, 7. Al igual que los sistemas de
numeración decimal y binario, este es un sistema posicional, por lo
cual en el sistema octal todos los procedimientos son  similares a los
que utilizamos con el sistema binario. El valor de posición en este
sistema se consigue multiplicando el digito por una potencia de 8.
EJEMPLO DE SISTEMA OCTAL •
979 1 7 23 8 = 1*3 = 3 8 = 8*2 = 16 8 = 64*7 = 448 8 = 512*1 = 512
979

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​​

​SISTEMA HEXADECIMAL

El sistema numérico hexadecimal o sistema hexadecimal (a veces
abreviado como  Hex, no confundir con  sistema sexagesimal) es un
sistema de numeración que emplea 16 símbolos. Su uso actual está
muy vinculado a la informática y ciencias de la computación.
En principio, dado que el sistema usual de numeración es de base
decimal y, por ello, sólo se dispone de diez dígitos, se adoptó  la
convención de usar las seis primeras letras del alfabeto latino para
suplir los dígitos que nos faltan. El conjunto de símbolos sería, por
tanto, el siguiente:
S=(0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.)
Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En
ocasiones se emplean letras minúsculas en lugar de mayúsculas.
Como en cualquier sistema de numeración posicional, el valor
numérico de cada dígito es alterado dependiendo de su posición en la
cadena de dígitos, quedando multiplicado por una cierta potencia de la
base del sistema, que en este caso es 16
Ejemplo:3E0A16 = 3×16
3
+ E×16
2
+ 0×16
1
+ A×16
0
= 3×4096 + 14×256 + 0×16
+ 10×1 = 15882.